Posted by Terence Tao
https://terrytao.wordpress.com/2025/12/08/the-story-of-erdos-problem-126/
http://terrytao.wordpress.com/?p=15920
Problem 1026 on the Erdős problem web site recently got solved through an interesting combination of existing literature, online collaboration, and AI tools. The purpose of this blog post is to try to tell the story of this collaboration, and also to supply a complete proof.
The original problem of Erdős, posed in 1975, is rather ambiguous. Erdős starts by recalling his famous theorem with Szekeres that says that given a sequence of  distinct real numbers, one can find a subsequence of length
distinct real numbers, one can find a subsequence of length  which is either increasing or decreasing; and that one cannot improve the
which is either increasing or decreasing; and that one cannot improve the  to
to 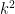 , by considering for instance a sequence of
, by considering for instance a sequence of  blocks of length
blocks of length  , with the numbers in each block decreasing, but the blocks themselves increasing. He also noted a result of Hanani that every sequence of length
, with the numbers in each block decreasing, but the blocks themselves increasing. He also noted a result of Hanani that every sequence of length  can be decomposed into the union of
can be decomposed into the union of  monotone sequences. He then wrote “As far as I know the following question is not yet settled. Let
monotone sequences. He then wrote “As far as I know the following question is not yet settled. Let  be a sequence of distinct numbers, determine
be a sequence of distinct numbers, determine

where the maximum is to be taken over all monotonic sequences

“.
This problem was added to the Erdős problem site on September 12, 2025, with a note that the problem was rather ambiguous. For any fixed  , this is an explicit piecewise linear function of the variables
, this is an explicit piecewise linear function of the variables  that could be computed by a simple brute force algorithm, but Erdős was presumably seeking optimal bounds for this quantity under some natural constraint on the
that could be computed by a simple brute force algorithm, but Erdős was presumably seeking optimal bounds for this quantity under some natural constraint on the  . The day the problem was posted, Desmond Weisenberg proposed studying the quantity
. The day the problem was posted, Desmond Weisenberg proposed studying the quantity 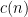 , defined as the largest constant such that
, defined as the largest constant such that

for all choices of (distinct) real numbers

. Desmond noted that for this formulation one could assume without loss of generality that the

were positive, since deleting negative or vanishing

does not decrease the left-hand side and does not increase the right-hand side. By a limiting argument one could also allow collisions between the

, so long as one interpreted monotonicity in the weak sense.
Though not stated on the web site, one can formulate this problem in game theoretic terms. Suppose that Alice has a stack of  coins for some large
coins for some large  . She divides the coins into
. She divides the coins into  piles of consisting of
piles of consisting of  coins each, so that
coins each, so that  . She then passes the piles to Bob, who is allowed to select a monotone subsequence of the piles (in the weak sense) and keep all the coins in those piles. What is the largest fraction
. She then passes the piles to Bob, who is allowed to select a monotone subsequence of the piles (in the weak sense) and keep all the coins in those piles. What is the largest fraction 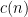 of the coins that Bob can guarantee to keep, regardless of how Alice divides up the coins? (One can work with either a discrete version of this problem where the
of the coins that Bob can guarantee to keep, regardless of how Alice divides up the coins? (One can work with either a discrete version of this problem where the  are integers, or a continuous one where the coins can be split fractionally, but in the limit
are integers, or a continuous one where the coins can be split fractionally, but in the limit 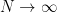 the problems can easily be seen to be equivalent.)
the problems can easily be seen to be equivalent.)
For small  , one can work this out by hand. For
, one can work this out by hand. For 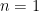 , clearly
, clearly  : Alice has to put all the coins into one pile, which Bob simply takes. Similarly
: Alice has to put all the coins into one pile, which Bob simply takes. Similarly  : regardless of how Alice divides the coins into two piles, the piles will either be increasing or decreasing, so in either case Bob can take both. The first interesting case is
: regardless of how Alice divides the coins into two piles, the piles will either be increasing or decreasing, so in either case Bob can take both. The first interesting case is 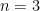 . Bob can again always take the two largest piles, guaranteeing himself
. Bob can again always take the two largest piles, guaranteeing himself  of the coins. On the other hand, if Alice almost divides the coins evenly, for instance into piles
of the coins. On the other hand, if Alice almost divides the coins evenly, for instance into piles  for some small
for some small 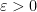 , then Bob cannot take all three piles as they are non-monotone, and so can only take two of them, allowing Alice to limit the payout fraction to be arbitrarily close to
, then Bob cannot take all three piles as they are non-monotone, and so can only take two of them, allowing Alice to limit the payout fraction to be arbitrarily close to  . So we conclude that
. So we conclude that  .
.
An hour after Desmond’s comment, Stijn Cambie noted (though not in the language I used above) that a similar construction to the one above, in which Alice divides the coins into 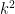 pairs that are almost even, in such a way that the longest monotone sequence is of length
pairs that are almost even, in such a way that the longest monotone sequence is of length  , gives the upper bound
, gives the upper bound  . It is also easy to see that
. It is also easy to see that 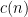 is a non-increasing function of
is a non-increasing function of  , so this gives a general bound
, so this gives a general bound  . Less than an hour after that, Wouter van Doorn noted that the Hanani result mentioned above gives the lower bound
. Less than an hour after that, Wouter van Doorn noted that the Hanani result mentioned above gives the lower bound  , and posed the problem of determining the asymptotic limit of
, and posed the problem of determining the asymptotic limit of  as
as 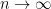 , given that this was now known to range between
, given that this was now known to range between  and
and  . This version was accepted by Thomas Bloom, the moderator of the Erdős problem site, as a valid interpretation of the original problem.
. This version was accepted by Thomas Bloom, the moderator of the Erdős problem site, as a valid interpretation of the original problem.
The next day, Stijn computed the first few values of 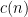 exactly:
exactly:

While the general pattern was not yet clear, this was enough for Stijn to conjecture that

, which would also imply that

as
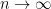
. (EDIT: as later located by an AI deep research tool, this conjecture was also made in Section 12 of
this 1980 article of Steele.) Stijn also described the extremizing sequences for this range of

, but did not continue the calculation further (a naive computation would take runtime exponential in

, due to the large number of possible subsequences to consider).
The problem then lay dormant for almost two months, until December 7, 2025, in which Boris Alexeev, as part of a systematic sweep of the Erdős problems using the AI tool Aristotle, was able to get this tool to autonomously solve this conjecture  in the proof assistant language Lean. The proof converted the problem to a rectangle-packing problem.
in the proof assistant language Lean. The proof converted the problem to a rectangle-packing problem.
This was one further addition to a recent sequence of examples where an Erdős problem had been automatically solved in one fashion or another by an AI tool. Like the previous cases, the proof turned out to not be particularly novel. Within an hour, Koishi Chan gave an alternate proof deriving the required bound  from the original Erdős-Szekeres theorem by a standard “blow-up” argument which we can give here in the Alice-Bob formulation. Take a large
from the original Erdős-Szekeres theorem by a standard “blow-up” argument which we can give here in the Alice-Bob formulation. Take a large 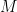 , and replace each pile of
, and replace each pile of  coins with
coins with  new piles, each of size
new piles, each of size  , chosen so that the longest monotone subsequence in this collection is
, chosen so that the longest monotone subsequence in this collection is  . Among all the new piles, the longest monotone subsequence has length
. Among all the new piles, the longest monotone subsequence has length  . Applying Erdős-Szekeres, one concludes the bound
. Applying Erdős-Szekeres, one concludes the bound

and on canceling the
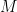
‘s, sending

, and applying Cauchy-Schwarz, one obtains

(in fact the argument gives

for all

).
Once this proof was found, it was natural to try to see if it had already appeared in the literature. AI deep research tools have successfully located such prior literature in the past, but in this case they did not succeed, and a more “old-fashioned” Google Scholar job turned up some relevant references: a 2016 paper by Tidor, Wang and Yang contained this precise result, citing an earlier paper of Wagner as inspiration for applying “blowup” to the Erdős-Szekeres theorem.
But the story does not end there! Upon reading the above story the next day, I realized that the problem of estimating 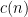 was a suitable task for AlphaEvolve, which I have used recently as mentioned in this previous post. Specifically, one could task to obtain upper bounds on
was a suitable task for AlphaEvolve, which I have used recently as mentioned in this previous post. Specifically, one could task to obtain upper bounds on 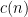 by directing it to produce real numbers (or integers)
by directing it to produce real numbers (or integers)  summing up to a fixed sum (I chose
summing up to a fixed sum (I chose 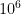 ) with a small a value of
) with a small a value of  as possible. After an hour of run time, AlphaEvolve produced the following upper bounds on
as possible. After an hour of run time, AlphaEvolve produced the following upper bounds on 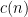 for
for  , with some intriguingly structured potential extremizing solutions:
, with some intriguingly structured potential extremizing solutions:

The scores, divided by
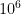
were pretty obviously trying to approximate rational numbers. There were a variety of ways (including modern AI) to extract the actual rational numbers they were close to, but I searched for a dedicated tool and found this useful
little web page of John Cook that did the job:

I could not immediately see the pattern here, but after some trial and error in which I tried to align numerators and denominators, I eventually organized this sequence into a more suggestive form:




which suggested a somewhat complicated but predictable conjecture for the values of the sequence
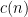
. On posting this, Boris found a clean formulation of the conjecture, namely that

whenever
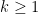
and

. After a bit of effort, he also produced an explicit upper bound construction:
Proposition 1 If 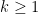 and
and  , then
, then  .
.
Proof: Consider a sequence  of numbers clustered around the “red number”
of numbers clustered around the “red number” 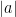 and “blue number”
and “blue number”  , consisting of
, consisting of 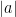 blocks of
blocks of  “blue” numbers, followed by
“blue” numbers, followed by  blocks of
blocks of  “red” numbers, and then
“red” numbers, and then  further blocks of
further blocks of  “blue” numbers, where all blocks are slightly increasing within each block, but the blue blocks are decreasing between each other, and the red blocks are decreasing between each other. The total number of elements is indeed
“blue” numbers, where all blocks are slightly increasing within each block, but the blue blocks are decreasing between each other, and the red blocks are decreasing between each other. The total number of elements is indeed

and the total sum is close to

With this setup, one can check that any monotone sequence consists either of at most

red elements and at most

blue elements, or no red elements and at most

blue element, in either case giving a monotone sum that is bounded by either

or

giving the claim.

Shortly afterwards, Lawrence Wu clarified the connection between this problem and a square packing problem, which was also due to Erdős (Problem 106). Let 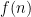 be the least number such that, whenever one packs
be the least number such that, whenever one packs  squares of sidelength
squares of sidelength  into a square of sidelength
into a square of sidelength 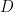 , with all sides parallel to the coordinate axes, one has
, with all sides parallel to the coordinate axes, one has

Proposition 2 For any  , one has
, one has 
Proof: Given  and
and 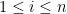 , let
, let 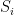 be the maximal sum over all increasing subsequences ending in
be the maximal sum over all increasing subsequences ending in  , and
, and 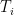 be the maximal sum over all decreasing subsequences ending in
be the maximal sum over all decreasing subsequences ending in  . For
. For  , we have either
, we have either  (if
(if  ) or
) or  (if
(if  ). In particular, the squares
). In particular, the squares  and
and  are disjoint. These squares pack into the square
are disjoint. These squares pack into the square ![{[0, S(x_1,\dots,x_n)]^2}](https://s0.wp.com/latex.php?latex=%7B%5B0%2C+S%28x_1%2C%5Cdots%2Cx_n%29%5D%5E2%7D&bg=ffffff&fg=000000&s=0&c=20201002) , so by definition of
, so by definition of  , we have
, we have

and the claim follows.

This idea of using packing to prove Erdős-Szekeres type results goes back to a 1959 paper of Seidenberg.
At this point, Lawrence performed another AI deep research search, this time successfully locating a paper from just last year by Baek, Koizumi, and Ueoro, where they show that
Theorem 3 For any 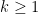 , one has
, one has 
which, when combined with a previous argument of Praton, implies
Theorem 4 For any 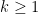 and
and  with
with  , one has
, one has 
This proves the conjecture!
There just remained the issue of putting everything together. I did feed all of the above information into a large language model, which was able to produce a coherent proof of (1) assuming the results of Baek-Koizumi-Ueoro and Praton. Of course, LLM outputs are prone to hallucination, so it would be preferable to formalize that argument in Lean, but this looks quite doable with current tools, and I expect this to be accomplished shortly. But I was also able to reproduce the arguments of Baek-Koizumi-Ueoro and Praton, which I include below for completeness.
Proof: (Proof of Theorem 3) We can normalize  . It then suffices to show that if we pack the length
. It then suffices to show that if we pack the length  torus
torus  by
by  axis-parallel squares of sidelength
axis-parallel squares of sidelength  , then
, then

Pick  . Then we have a
. Then we have a 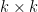 grid
grid

inside the torus. The
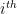
square, when restricted to this grid, becomes a discrete rectangle

for some finite sets

with

By the packing condition, we have

From
(2) we have

hence

Inserting this bound and rearranging, we conclude that

Taking the supremum over

we conclude that

so by the pigeonhole principle one of the summands is at most
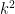
. Let’s say it is the former, thus

In particular, the average value of

is at most
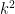
. But this can be computed to be

, giving the claim. Similarly if it is the other sum.

Proof: (Proof of Theorem 4) We write  with
with  . We can rescale so that the square one is packing into is
. We can rescale so that the square one is packing into is ![{[0,k]^2}](https://s0.wp.com/latex.php?latex=%7B%5B0%2Ck%5D%5E2%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Thus, we pack
. Thus, we pack  squares of sidelength
squares of sidelength  into
into ![{[0,k]^2}](https://s0.wp.com/latex.php?latex=%7B%5B0%2Ck%5D%5E2%7D&bg=ffffff&fg=000000&s=0&c=20201002) , and our task is to show that
, and our task is to show that

We pick a large natural number

(in particular, larger than

), and consider the three nested squares
![\displaystyle [0,k]^2 \subset [0,N]^2 \subset [0,N + |c| \frac{N}{N-\varepsilon}]^2.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5B0%2Ck%5D%5E2+%5Csubset+%5B0%2CN%5D%5E2+%5Csubset+%5B0%2CN+%2B+%7Cc%7C+%5Cfrac%7BN%7D%7BN-%5Cvarepsilon%7D%5D%5E2.&bg=ffffff&fg=000000&s=0&c=20201002)
We can pack
![{[0,N]^2 \backslash [0,k]^2}](https://s0.wp.com/latex.php?latex=%7B%5B0%2CN%5D%5E2+%5Cbackslash+%5B0%2Ck%5D%5E2%7D&bg=ffffff&fg=000000&s=0&c=20201002)
by

unit squares. We can similarly pack
![\displaystyle [0,N + |c| \frac{N}{N-\varepsilon}]^2 \backslash [0,N]^2](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5B0%2CN+%2B+%7Cc%7C+%5Cfrac%7BN%7D%7BN-%5Cvarepsilon%7D%5D%5E2+%5Cbackslash+%5B0%2CN%5D%5E2&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle [0, \frac{N}{N-\varepsilon} (N+|c|-\varepsilon)]^2 \backslash [0, \frac{N}{N-\varepsilon} (N-\varepsilon)]^2](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5B0%2C+%5Cfrac%7BN%7D%7BN-%5Cvarepsilon%7D+%28N%2B%7Cc%7C-%5Cvarepsilon%29%5D%5E2+%5Cbackslash+%5B0%2C+%5Cfrac%7BN%7D%7BN-%5Cvarepsilon%7D+%28N-%5Cvarepsilon%29%5D%5E2&bg=ffffff&fg=000000&s=0&c=20201002)
into

squares of sidelength

. All in all, this produces

squares, of total length

Applying Theorem
3, we conclude that


The right-hand side is

and the left-hand side similarly evaluates to

and so we simplify to

Sending
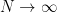
, we obtain the claim.

https://terrytao.wordpress.com/2025/12/08/the-story-of-erdos-problem-126/
http://terrytao.wordpress.com/?p=15920